Page 82 - 理化检验-化学分册 2021年第六期
P. 82
李 怿, 等: 以留样再测为基础的实验室质量控制
其中 K 为参考值, 通常在目标值 μ 0 和失控值 μ 1 之
间, 一般 取 实 验 室 中 间 精 密 度 的 倍 数. 当 统 计 量
C i 和C i 超出判定区间 H 时, 考虑测试系统运行
-
+
失控. h 和 f 是判定规则参数, 它们的选择与实验
室确定的临界值、 平均运行长度等因素有关, 本文选
择可以更快检测出异常的 CS2 方案 [ 9 ] , 即 h=3.5 ,
f 2=0.5 , 此时平均链长为 140~200 , 临界漂移介
/
于 0.75σ site 和 1.5σ site 之间.表 3 是应用 CUSUM 表
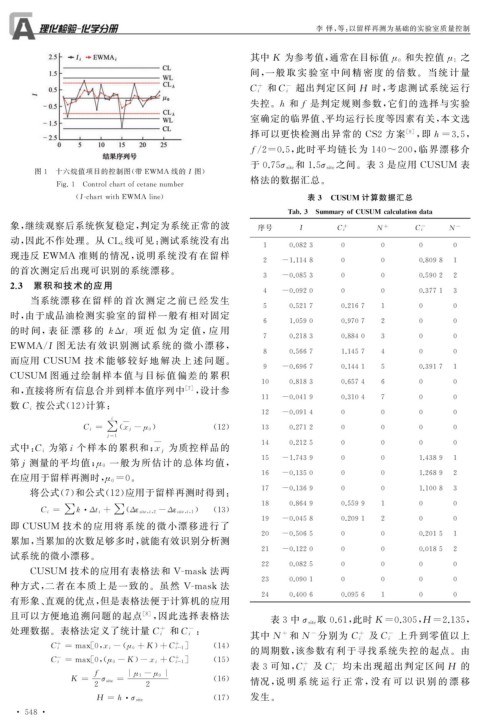
图 1 十六烷值项目的控制图( 带 EWMA 线的I 图)
格法的数据汇总.
Fi g .1 Controlchartofcetanenumber
( IGchartwithEWMAline ) 表 3 CUSUM 计算数据汇总
Tab.3 Summar y ofCUSUMcalculationdata
象, 继续观察后系统恢复稳定, 判定为系统正常的波 序号 I C i + N + C i - N -
动, 因此不作处理.从 CL λ 线可见: 测试系统没有出
1 0.0823 0 0 0 0
现违反 EWMA 准则的情况, 说明系统没有在留样
2 -1.1148 0 0 0.8098 1
的首次测定后出现可识别的系统漂移.
3 -0.0853 0 0 0.5902 2
2.3 累积和技术的应用
4 -0.0920 0 0 0.3771 3
当系统漂移在留样的首次测定之前已经 发生
5 0.5217 0.2167 1 0 0
时, 由于成品油检测实验室的留样一般有相对固定
6 1.0590 0.9707 2 0 0
的时 间, 表 征 漂 移 的 kΔt i 项 近 似 为 定 值, 应 用
7 0.2183 0.8840 3 0 0
EWMA / I 图无法有效识别测试 系统的微小漂移,
8 0.5667 1.1457 4 0 0
而应用 CUSUM 技 术 能 够 较 好 地 解 决 上 述 问 题.
9 -0.6967 0.1441 5 0.3917 1
CUSUM 图通过绘制样本值与目 标 值 偏 差 的 累 积
10 0.8183 0.6574 6 0 0
和, 直接将所有信息合并到样本值序列中 [ 7 ] , 设计参
11 -0.0419 0.3104 7 0 0
数 C i 按公式( 12 ) 计算:
12 -0.0914 0 0 0 0
i
C i = ∑ ( x j - μ 0 ) ( 12 ) 13 0.2712 0 0 0 0
j= 1
为质控样品的 14 0.2125 0 0 0 0
式中: C i 为第 i 个样本的累积和; x j
15 -1.7439 0 0 1.4389 1
μ 0 一般为所估计的总体均值,
第 j 测量的平均值;
16 -0.1350 0 0 1.2689 2
μ 0=0 .
在应用于留样再测时,
17 -0.1369 0 0 1.1008 3
将公式( 7 ) 和公式( 12 ) 应用于留样再测时得到:
18 0.8649 0.5599 1 0 0
C i = ∑ k Δt i + ∑ ( Δε site , i , 2 -Δε site , i , 1 ) ( 13 )
19 -0.0458 0.2091 2 0 0
即 CUSUM 技术的应用将系统的微小漂移进行了
20 -0.5065 0 0 0.2015 1
累加, 当累加的次数足够多时, 就能有效识别分析测
21 -0.1220 0 0 0.0185 2
试系统的微小漂移.
CUSUM 技术的应用有表格法和 VGmask 法两 22 0.0825 0 0 0 0
23 0.0901 0 0 0 0
种方式, 二者在本质上是一致的.虽然 VGmask 法
24 0.4006 0.0956 1 0 0
有形象、 直观的优点, 但是表格法便于计算机的应用
且可以方便地追溯问题的起点 [ 8 ] , 因此选择表格法
表 3 中σ site 取 0.61 , 此时 K=0.305 , H =2.135 ,
+ - :
其中 N 和 N 分别为 C i 及C i 上升到零值以上
-
+
+
处理数据.表格法定义了统计量 C i 和C i
-
+
+
C i = max [ 0 , x i - ( 0 +K ) +C i - 1 ] ( 14 ) 的周期数, 该参数有利于寻找系统失控的起点.由
μ
-
+
C i = max [ 0 ,( 0 -K ) -x i +C i - 1 ] ( 15 )
μ
表 3 可知, C i 及C i 均未出现超出判定区间 H 的
+
-
f | μ 1 - μ 0|
K = σ site = ( 16 ) 情况, 说 明 系 统 运 行 正 常, 没 有 可 以 识 别 的 漂 移
2 2
( 17 ) 发生.
H =h σ site
5 4 8